Nathan Jensen is a Postdoctoral Associate at Cornell’s Dyson School who is working with the International Livestock Research Institute (ILRI).
The phrases “stuck in poverty” and “fell into poverty” are often used in the popular press, reports and journal articles. These phrases draw on poverty trap theory—the idea that poverty can be reinforcing, so that freeing oneself from poverty can be more difficult than other similar changes to wealth status. For those of us working to reduce poverty, understanding such nonlinearities in wealth dynamics and identifying thresholds in those dynamics is critical for success.
Poverty trap research aims to understand how wealth (or another variable of interest) progresses over time. Empirical studies have found some societies in which there appear to be two wealth equilibria separated by a threshold. The threshold separates those who are pulled towards the low (poorer) equilibria, and those who are pulled towards the high (wealthier) equilibria. Those individuals who find themselves below the threshold will be “trapped” because even small gains will quickly dissipate as they return to the lower welfare equilibrium. The opposite is true for individuals above the threshold. But, if the threshold is known, efforts can be made to help folks overcome it and to secure folks who are above but near it. In fact, much of the literature on social protection draws on these ideas of overcoming structural barriers to growth and reducing beneficiaries’ vulnerability to falling below certain thresholds.
The purpose of this post is to remind researchers and practitioners that the intertemporal dynamics of complex systems, such as those associated with household wealth, are often extremely sensitive to changes in the characteristics of that system. Because of this, the dynamics of wealth and poverty are likely to vary dramatically across environments and specific estimates of poverty trap thresholds should only be applied out of context with care.
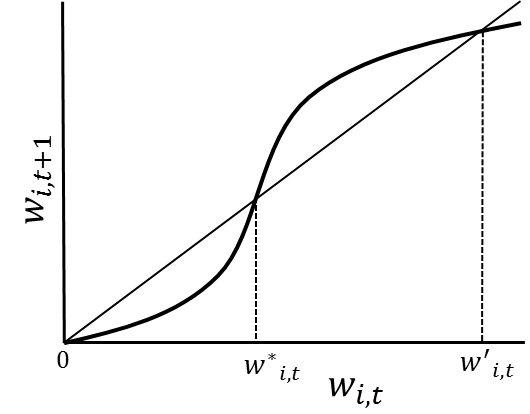
Empirically, intertemporal wealth dynamics are typically estimated by examining how expected future wealth varies across current wealth. To illustrate this point, I use the classic case of a multiple equilibrium poverty trap (Figure 1).

Note the “S” shaped curve reflecting the non-linear relationship between current wealth (wi,t on the x-axis) and next period’s wealth (wi,t+1 on the y-axis). Here, zero and w’i,t represent stable equilibria because households starting with an initial endowment below w* will converge to zero wealth, while those that initially fall above w*i,t will converge to w’i,t. This makes w*i,t a critical wealth threshold.
To model the above dynamics in reduced form requires a minimum of a cubed relationship between current and next period’s wealth.[1] Equation (1) meets such a minimum requirement where the βs are coefficients and ei,t is a stochastic error.
It is also reasonable to believe that environmental and household characteristics (xi,t) affect next period’s outcomes and that the sensitivity of outcomes to such characteristics are heterogeneous across wealth space. In that case, equation (1) can be rewritten with interactions between a polynomial of wealth, a vector of characteristics, and vectors of parameter estimates (α1,α2,α3) as equation (2).
Analytically, the critical wealth threshold for the equilibria dynamics represented in Figure 1 is the lower of the two non-zero solutions to the following:
Equation (3) illustrates that whenever outcomes are autocorrelated and interact with other factors (e.g., household characteristics, environment), thresholds will be a function of those factors. That is, any such threshold is likely to be specific to time, geography, and attributes. The context-specific nature of intertemporal dynamics holds for any outcome variable of interest (e.g., welfare, consumption) and for other numbers of equilibria so long as outcomes are a function of autoregressive interactions with other characteristics. This is not to draw into question the thresholds that have been identified empirically, which in the above example would be identified at the mean values of xi,t, but to remind our community of poverty researchers that applying specific thresholds across contexts should be done cautiously.
[1] Semi-parametric and nonparametric methods are often used when estimating inter-temporal dynamics to avoid making the functional form assumptions implied by equation (1). Those methods do not alleviate the issues discussed here.